Absolute Value in Algebra

Absolute Value means ...

... how far a number is from zero:

absolute value 6 either way

"6" is 6 away from zero,
and "−6" is also 6 away from zero.

So the absolute value of 6 is 6,
and the absolute value of −6 is also 6

Absolute Value Symbol

To show we want the absolute value we put "|" marks either side (called "bars"), like these examples:


vertical bar The "|" can be found just above the enter key on most keyboards.

More Formal

More formally we have:

Absolute Value

Which says the absolute value of x equals:

  • x when x is greater than zero
  • 0 when x equals 0
  • −x when x is less than zero (this "flips" the number back to positive)

So when a number is positive or zero we leave it alone, when it is negative we change it to positive using −x.

Example: what is |−17| ?

Well, it is less than zero, so we need to calculate "−x":

− ( −17 ) = +17

(Because two minuses make a plus)

Useful Properties

Here are some properties of absolute values that can be useful:

  • |a| ≥ 0 always!

    That makes sense ... |a| can never be less than zero.

  • |a| = √(a2)

    Squaring a makes it positive or zero (for a as a Real Number). Then taking the square root will "undo" the squaring, but leave it positive or zero.

  • |a × b| = |a| × |b|

    Means these are the same:

    • the absolute value of (a times b), and
    • (the absolute value of a) times (the absolute value of b)

    Which can also be useful when solving

  • |u| = a is the same as u = ±a and vice versa

    Which is often the key to solving most absolute value questions.

Example: Solve |x+2| = 5

Using "|u| = a is the same as u = ±a":

this: |x+2| = 5

is the same as this: x+2 = ±5

Which has two solutions:

x+2 = −5 x+2 = +5
x = −7 x = 3

Graphically

Let us graph that example:

|x+2| = 5

It is easier to graph when we have an "=0" equation, so subtract 5 from both sides:

|x+2| − 5 = 0

So now we can plot y=|x+2|−5 and find where it equals zero.

Here is the plot of y=|x+2|−5, but just for fun let's make the graph by shifting it around:

|x+2| - 5 = 0
Start with y=|x| then shift it left to make
it y=|x+2| 		then shift it down to make
it y=|x+2|−5

And the two solutions (circled) are −7 and +3.

Absolute Value Inequalities

Mixing Absolute Values and Inequalites needs a little care!

There are 4 inequalities:

< ≤ > ≥
less than less than
or equal to 		greater than greater than
or equal to

Less Than, Less Than or Equal To

With "<" and "≤" we get one interval centered on zero:

Example: Solve |x| < 3

This means the distance from x to zero must be less than 3:

-3 to 3

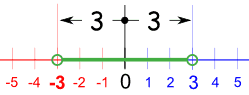
Everything in between (but not including) -3 and 3

It can be rewritten as:

−3 < x < 3

As an interval it can be written as:

(−3, 3)

The same thing works for "Less Than or Equal To":

Example: Solve |x| ≤ 3

Everything in between and including -3 and 3

It can be rewritten as:

−3 ≤ x ≤ 3

As an interval it can be written as:

[−3, 3]

How about a bigger example?

Example: Solve |3x-6| ≤ 12

Rewrite it as:

−12 ≤ 3x−6 ≤ 12

Add 6:

−6 ≤ 3x ≤ 18

Lastly, multiply by (1/3). Because we are multiplying by a positive number, the inequalities will not change:

−2 ≤ x ≤ 6

Done!

As an interval it can be written as:

[−2, 6]

Greater Than, Greater Than or Equal To

This is different ... we get two separate intervals:

Example: Solve |x| > 3

It looks like this:

|x| > 3

Up to -3 or from 3 onwards

It can be rewritten as

x < −3 or x > 3

As an interval it can be written as:

(−∞, −3) U (3, +∞)

Careful! Do not write it as

−3 > x > 3 no!

"x" cannot be less than -3 and greater than 3 at the same time

It is really:

x < −3 or x > 3 yes

"x" is less than −3 or greater than 3

The same thing works for "Greater Than or Equal To":

Example: Solve |x| ≥ 3

Can be rewritten as

x ≤ −3 or x ≥ 3

As an interval it can be written as:

(−∞, −3] U [3, +∞)